Einstein field equations
| General relativity | ||||||||||||
 |
||||||||||||
| Einstein field equations | ||||||||||||
| Introduction Mathematical formulation Resources
|
||||||||||||
The Einstein field equations (EFE) or Einstein's equations are a set of ten equations in Albert Einstein's theory of general relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy.[1] First published by Einstein in 1915[2] as a tensor equation, the EFE equate spacetime curvature (expressed by the Einstein tensor) with the energy and momentum within that spacetime (expressed by the stress-energy tensor).
Similar to the way that electromagnetic fields are determined using charges and currents via Maxwell's equations, the EFE are used to determine the spacetime geometry resulting from the presence of mass-energy and linear momentum, that is, they determine the metric tensor of spacetime for a given arrangement of stress-energy in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of non-linear partial differential equations when used in this way. The solutions of the EFE are the components of the metric tensor. The inertial trajectories of particles and radiation (geodesics) in the resulting geometry are then calculated using the geodesic equation.
As well as obeying local energy-momentum conservation, the EFE reduce to Newton's law of gravitation where the gravitational field is weak and velocities much less than the speed of light.[3]
Solution techniques for the EFE include simplifying assumptions such as symmetry. Special classes of exact solutions are most often studied as they model many gravitational phenomena, such as rotating black holes and the expanding universe. Further simplification is achieved in approximating the actual spacetime as flat spacetime with a small deviation, leading to the linearised EFE. These equations are used to study phenomena such as gravitational waves.
Contents |
Mathematical form
The Einstein field equations (EFE) may be written in the form:[1]
where  is the Ricci curvature tensor,
is the Ricci curvature tensor,  the scalar curvature,
the scalar curvature,  the metric tensor,
the metric tensor, 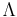 is the cosmological constant,
is the cosmological constant, 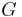 is Newton's gravitational constant,
is Newton's gravitational constant,  the speed of light, and
the speed of light, and  the stress-energy tensor.
the stress-energy tensor.
The EFE is a tensor equation relating a set of symmetric 4 x 4 tensors. It is written here using the abstract index notation. Each tensor has 10 independent components. Given the freedom of choice of the four spacetime coordinates, the independent equations reduce to 6 in number.
Although the Einstein field equations were initially formulated in the context of a four-dimensional theory, some theorists have explored their consequences in n dimensions. The equations in contexts outside of general relativity are still referred to as the Einstein field equations. The vacuum field equations define Einstein manifolds.
Despite the simple appearance of the equations they are, in fact, quite complicated. Given a specified distribution of matter and energy in the form of a stress-energy tensor, the EFE are understood to be equations for the metric tensor  , as both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE are a system of 10 coupled, nonlinear, hyperbolic-elliptic partial differential equations.
, as both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE are a system of 10 coupled, nonlinear, hyperbolic-elliptic partial differential equations.
One can write the EFE in a more compact form by defining the Einstein tensor
which is a symmetric second-rank tensor that is a function of the metric. The EFE can then be written as
where the cosmological term has been absorbed into the stress-energy tensor as dark energy.
Using geometrized units where G = c = 1, this can be rewritten as
The expression on the left represents the curvature of spacetime as determined by the metric and the expression on the right represents the matter/energy content of spacetime. The EFE can then be interpreted as a set of equations dictating how the curvature of spacetime is related to the matter/energy content of the universe.
These equations, together with the geodesic equation, form the core of the mathematical formulation of general relativity.
Sign convention
The above form of the EFE is the standard established by Misner, Thorne, and Wheeler. The authors analyzed all conventions that exist and classified according to the following three signs (S1, S2, S3):
The third sign above is related to the choice of convention for the Ricci tensor:
With these definitions Misner, Thorne, and Wheeler classify themselves as  , whereas Weinberg (1972) is
, whereas Weinberg (1972) is  , Peebles (1980) and Efstathiou (1990) are
, Peebles (1980) and Efstathiou (1990) are  while Peacock (1994), Rindler (1977), Atwater (1974), Collins Martin & Squires (1989) are
while Peacock (1994), Rindler (1977), Atwater (1974), Collins Martin & Squires (1989) are  .
.
Authors including Einstein have used a different sign in their definition for the Ricci tensor which results in the sign of the constant on the right side being negative
The sign of the (very small) cosmological term would change in both these versions, if the +--- metric sign convention is used rather than the MTW −+++ metric sign convention adopted here.
Equivalent formulations
The trace of the EFE is
which simplifies to
If one adds  times this to the EFE, one gets the following equivalent "trace-reversed" form
times this to the EFE, one gets the following equivalent "trace-reversed" form
Reversing the trace again would restore the original EFE. The trace-reversed form may be more convenient in some cases (for example, when one is interested in weak-field limit and can replace  in the expression on the right with the Minkowski metric without significant loss of accuracy).
in the expression on the right with the Minkowski metric without significant loss of accuracy).
The cosmological constant
Einstein modified his original field equations to include a cosmological term proportional to the metric
The constant  is the cosmological constant. Since
is the cosmological constant. Since  is constant, the energy conservation law is unaffected.
is constant, the energy conservation law is unaffected.
The cosmological constant term was originally introduced by Einstein to allow for a static universe (i.e., one that is not expanding or contracting). This effort was unsuccessful for two reasons: the static universe described by this theory was unstable, and observations of distant galaxies by Hubble a decade later confirmed that our universe is, in fact, not static but expanding. So  was abandoned, with Einstein calling it the "biggest blunder [he] ever made".[4] For many years the cosmological constant was almost universally considered to be 0.
was abandoned, with Einstein calling it the "biggest blunder [he] ever made".[4] For many years the cosmological constant was almost universally considered to be 0.
Despite Einstein's misguided motivation for introducing the cosmological constant term, there is nothing inconsistent with the presence of such a term in the equations. Indeed, recent improved astronomical techniques have found that a positive value of  is needed to explain some observations.[5][6]
is needed to explain some observations.[5][6]
Einstein thought of the cosmological constant as an independent parameter, but its term in the field equation can also be moved algebraically to the other side, written as part of the stress-energy tensor:
The vacuum energy is constant and given by
The existence of a cosmological constant is thus equivalent to the existence of a non-zero vacuum energy. The terms are now used interchangeably in general relativity.
Features
Conservation of energy and momentum
General relativity is consistent with the local conservation of energy and momentum expressed as
 .
.
Contracting the differential Bianchi identity
with  gives, using the fact that the metric tensor is covariantly constant, i.e.
gives, using the fact that the metric tensor is covariantly constant, i.e.  ,
,
The antisymmetry of the Riemann tensor allows the second term in the above expression to be rewritten:
which is equivalent to
using the definition of the Ricci tensor.
Next, contract again with the metric
to get
The definitions of the Riemann tensor and Ricci scalar then show that
which can be rewritten as
A final contraction with  gives
gives
which by the symmetry of the bracketed term and the definition of the Einstein tensor, gives, after relabelling the indices,
Using the EFE, this immediately gives,
which expresses the local conservation of stress-energy. This conservation law is a physical requirement. With his field equations Einstein ensured that general relativity is consistent with this conservation condition.
Nonlinearity
The nonlinearity of the EFE distinguishes general relativity from many other fundamental physical theories. For example, Maxwell's equations of electromagnetism are linear in the electric and magnetic fields, and charge and current distributions (i.e. the sum of two solutions is also a solution); another example is Schrödinger's equation of quantum mechanics which is linear in the wavefunction.
The correspondence principle
The EFE reduce to Newton's law of gravity by using both the weak-field approximation and the slow-motion approximation. In fact, the constant appearing in the EFE is determined by making these two approximations.
Newtonian gravitation can be written as the theory of a scalar field,  , which is the gravitational potential in joules per kilogram
, which is the gravitational potential in joules per kilogram
where  is the mass density. The orbit of a free-falling particle satisfies
is the mass density. The orbit of a free-falling particle satisfies
In tensor notation, these become
In general relativity, these equations are replaced by the Einstein field equations in the trace-reversed form
for some constant, K, and the geodesic equation
To see how the latter reduce to the former, we assume that the test particle's velocity is approximately zero
and thus
and that the metric and its derivatives are approximately static and that the squares of deviations from the Minkowski metric are negligible. Applying these simplifying assumptions to the spatial components of the geodesic equation gives
where two factors of  have been divided out. This will reduce to its Newtonian counterpart, provided
have been divided out. This will reduce to its Newtonian counterpart, provided
Our assumptions force α=i and the time (0) derivatives to be zero. So this simplifies to
which is satisfied by letting
Turning to the Einstein equations, we only need the time-time component
the low speed and static field assumptions imply that
So
and thus
From the definition of the Ricci tensor
Our simplifying assumptions make the squares of Γ disappear together with the time derivatives
Combining the above equations together
which reduces to the Newtonian field equation provided
which will occur if
Vacuum field equations

If the energy-momentum tensor 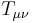 is zero in the region under consideration, then the field equations are also referred to as the vacuum field equations. By setting
is zero in the region under consideration, then the field equations are also referred to as the vacuum field equations. By setting 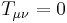 in the full field equations, the vacuum equations can be written as
in the full field equations, the vacuum equations can be written as
Taking the trace of this (contracting with  ) and using the fact that
) and using the fact that 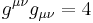 , we get
, we get
and thus
Substituting back, we get an equivalent form of the vacuum field equations
In the case of nonzero cosmological constant, the equations are
which gives
yielding the equivalent form
The solutions to the vacuum field equations are called vacuum solutions. Flat Minkowski space is the simplest example of a vacuum solution. Nontrivial examples include the Schwarzschild solution and the Kerr solution.
Manifolds with a vanishing Ricci tensor,  , are referred to as Ricci-flat manifolds and manifolds with a Ricci tensor proportional to the metric as Einstein manifolds.
, are referred to as Ricci-flat manifolds and manifolds with a Ricci tensor proportional to the metric as Einstein manifolds.
Einstein–Maxwell equations
If the energy-momentum tensor 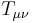 is that of an electromagnetic field in free space, i.e. if the electromagnetic stress-energy tensor
is that of an electromagnetic field in free space, i.e. if the electromagnetic stress-energy tensor
is used, then the Einstein field equations are called the Einstein–Maxwell equations (with cosmological constant Λ, taken to be zero in conventional relativity theory):
Additionally, the covariant Maxwell Equations are also applicable in free space:
where the semicolon represents a covariant derivative, and the brackets denote anti-symmetrization. The first equation asserts that the 4-divergence of the two-form F is zero, and the second that its exterior derivative is zero. From the latter, it follows by the Poincaré lemma that in a coordinate chart it is possible to introduce an electromagnetic field potential Aα such that
in which the comma denotes a partial derivative. This is often taken as equivalent to the covariant Maxwell equation from which it is derived.[7] However, there are global solutions of the equation which may lack a globally defined potential.[8]
Solutions
The solutions of the Einstein field equations are metrics of spacetime. The solutions are hence often called 'metrics'. These metrics describe the structure of the spacetime including the inertial motion of objects in the spacetime. As the field equations are non-linear, they cannot always be completely solved (i.e. without making approximations). For example, there is no known complete solution for a spacetime with two massive bodies in it (which is a theoretical model of a binary star system, for example). However, approximations are usually made in these cases. These are commonly referred to as post-Newtonian approximations. Even so, there are numerous cases where the field equations have been solved completely, and those are called exact solutions.[9]
The study of exact solutions of Einstein's field equations is one of the activities of cosmology. It leads to the prediction of black holes and to different models of evolution of the universe.
The linearised EFE
The nonlinearity of the EFE makes finding exact solutions difficult. One way of solving the field equations is to make an approximation, namely, that far from the source(s) of gravitating matter, the gravitational field is very weak and the spacetime approximates that of Minkowski space. The metric is then written as the sum of the Minkowski metric and a term representing the deviation of the true metric from the Minkowski metric. This linearisation procedure can be used to discuss the phenomena of gravitational radiation.
See also
|
|
References
See General relativity resources.
- ↑ 1.0 1.1 Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik. http://www.alberteinstein.info/gallery/gtext3.html.
- ↑ Einstein, Albert (November 25, 1915). "Die Feldgleichungen der Gravitation". Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844–847. http://nausikaa2.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.x.cgi?dir=6E3MAXK4&step=thumb. Retrieved 2006-09-12.
- ↑ Carroll, Sean (2004). Spacetime and Geometry - An Introduction to General Relativity. pp. 151–159. ISBN 0-8053-8732-3.
- ↑ Gamow, George (April 28, 1970). My World Line : An Informal Autobiography. Viking Adult. ISBN 0670503762. http://www.jb.man.ac.uk/~jpl/cosmo/blunder.html. Retrieved 2007-03-14.
- ↑ Wahl, Nicolle (2005-11-22). "Was Einstein's 'biggest blunder' a stellar success?". http://www.news.utoronto.ca/bin6/051122-1839.asp. Retrieved 2007-03-14.
- ↑ Turner, Michael S. (May, 2001). "A Spacetime Odyssey". Int.J.Mod.Phys. A17S1: 180–196. http://arxiv.org/abs/astro-ph/0202008. Retrieved 2007-03-14.
- ↑ Brown, Harvey (2005). Physical Relativity. Oxford University Press. p. 164. ISBN 9780199275830. http://books.google.com/?id=T6IVyWiPQksC&pg=PA164&dq=Maxwell+and+potential+and+%22generally+covariant%22.
- ↑ Trautman, Andrzej (1977). "Solutions of the Maxwell and Yang-Mills equations associated with hopf fibrings". International Journal of Theoretical Physics 16 (9): 561–565. doi:10.1007/BF01811088..
- ↑ Stephani, Hans; D. Kramer, M. MacCallum, C. Hoenselaers and E. Herlt (2003). Exact Solutions of Einstein's Field Equations. Cambridge University Press. ISBN 0-521-46136-7.
- Aczel, Amir D., 1999. God's Equation: Einstein, Relativity, and the Expanding Universe. Delta Science. A popular account.
- Charles Misner, Kip Thorne, and John Wheeler, 1973. Gravitation. W H Freeman.
External links
- Caltech Tutorial on Relativity — A simple introduction to Einstein's Field Equations.
- The Meaning of Einstein's Equation — An explanation of Einstein's field equation, its derivation, and some of its consequences
- Video Lecture on Einstein's Field Equations by MIT Physics Professor Edmund Bertschinger.




![g_{\mu \nu}~~=[S1] \times \operatorname{diag}(-1,+1,+1,+1)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ac9fa8b1a249ac1a5f78da8f6bc365d7.png)
![{R^\mu}_{a \beta \gamma}=[S2] \times (\Gamma^\mu_{a \gamma,\beta}-\Gamma^\mu_{a \beta,\gamma}+\Gamma^\mu_{\sigma \beta}\Gamma^\sigma_{\gamma a}-\Gamma^\mu_{\sigma \gamma}\Gamma^\sigma_{\beta a})](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ad7e5826a4a4867bc422065f07658a2f.png)
![G_{\mu \nu}~~=[S3] \times {8 \pi G \over c^4} T_{\mu \nu}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5b9a11a28b24aafc4d8bcfde8213e059.png)
![R_{\mu \nu}=[S2]\times [S3] \times {R^a}_{\mu a \nu}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/67712c87e2988b00574d6074416b340f.png)


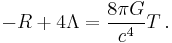
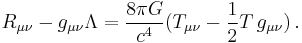



![R_{ab[cd;e]} = \, 0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/f4fb36895ca1ad0ce1e0a13df3693ec3.png)
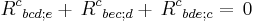








![\nabla^2 \Phi [\vec{x},t] = 4 \pi G \rho [\vec{x},t]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8d162e02fb3d4c0a4ece06782e43b860.png)
![\ddot{\vec{x}}[t] = - \nabla \Phi [\vec{x} [t],t] \,.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d6ad46f2e62b895c4ac0e2769fbada1f.png)

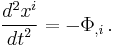







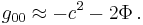















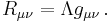
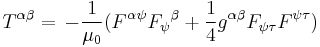


![F_{[\alpha\beta;\gamma]}=\frac{1}{3}\left(F_{\alpha\beta;\gamma} + F_{\beta\gamma;\alpha}+F_{\gamma\alpha;\beta}\right) = 0. \!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9aab3bd95a5046c415cd90da72dea4a7.png)
